last update 01/10/2009

Yakovlev Fedor Home-page to first page *: yak@ifz.ru

FOLDING formation research Guide: about the study of folded structures of several scale levels into thin-layered flysch-like sediments in a Hinterland

III. LOCALE STRUCTURES AND THEIR MECHANISMS ANALYSIS USING THE STRAIN ELLIPSOID OF DOMAINS

8. Strain ellipsoid of a fold and of a folded domain (ranks 2, 3) – since 1987.

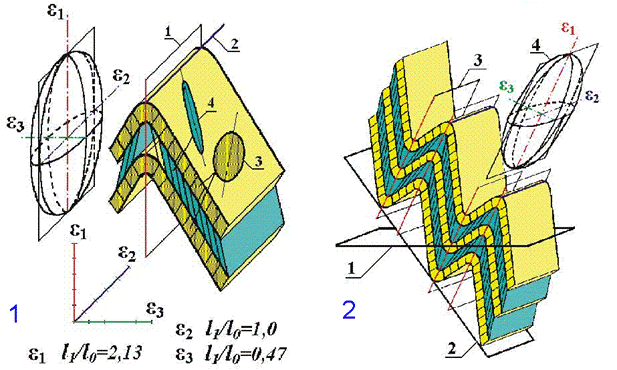
·Description. There is famous difficulty to generalize the data of strain-analysis to scale of one fold and larger size objects. The reason is a heterogeneity of strain.  The solution was found in application of model of multilayer folds formation (point 7) for this problem. The shortening value of fold is calculated not for horizontal direction but for perpendicular to axial surface (fig. 1). Thus the ellipsoid of deformation relates to shortening value of folds and to orientation of axial surface. Maximal length axis possesses to axial plain and it perpendicular to hinge line, minimal length axis is perpendicular to hinge line and to axial surface, intermediate length axis is hinge line. For a folded domain important parameters (fig. 2) are A) axial plain dip (3), B) folds envelope plane dip (2), fold shortening value (fold strain ellipse shortening, 4). An orientation of envelope surface of folds (2, fig. 2) is important as orientation of initial horizontal position of prefolded layering in isomeric volume. Such generalization may be used for several aims on next steps of study: meso-scale mechanisms formation elucidation, retro-deformation of structural sections (balancing of section) and so on.

·Publications. First publication which used in fact this idea was paper (Yakovlev F.L. “A Study of the Kinematic...”, 1987; (PDF), N 3 in List-En). The topic is discussed also in: (Yakovlev F.L. “Investigation of the processes …”, 2002; PDF-R, N 9 in List-En). The especial description of topic was short paper (Yakovlev F.L., Voitenko V.N. “Application of the deformation...”, 2005; PDF, N 11 in List-En).

Fig. 1 The ellipsoid of strain for a fold. 1 – axial surface (ε1), 2- hinge line (ε2), (ε3)– shortening value Sh; 3 – strain ellipse for competent layer; 4 – strain ellipse for incompetent layer

Fig. 1 The ellipsoid of strain for folded domain (Ax – axial surface dip(3), En –envelope surface dip(2), Sh – shortening value (4, ε3). 1 - horizontal plain.

© 2009, ИФЗ РАН, Яковлев