Guide-yak-e-3.RU

last update

07/10/2009

Yakovlev Fedor

Home-page

FOLDING formation research

Guide:

about the study of folded structures of several scale levels into thin-layered flysch-like sediments in a Hinterland

I. THE THEORETICAL BASEMENT

3. Multi-rank strain analysis of linear folded structures – since 2008

Description. New principle for defining objects of linear folding and determining mechanisms of its formation has been offered. According to this principle, boundaries between structures should be drawn so that the volume of the defined object is embraced by a single deformation mechanism. 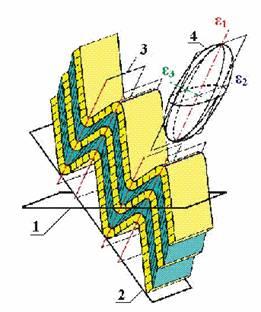The objects can be outlined based on traditional morphological classifications of structural geology only when they are characterized by a single and complete formation mechanism (Fig. 1). 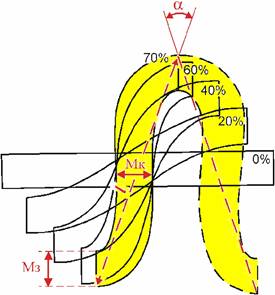Cinematic models of forming, which include description of changes of main parameters of object geometry are offering (Fig. 2). This model is describing also the strain parameters of intra-layer object (for usual strain-analysis). 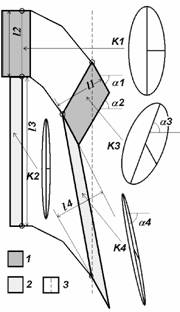These models are using for solutions of reverse problems, including the finding out of shortening value (Fig. 3). The previously proposed hierarchy of linear folded structures, which include seven structural ranks with their own specific sets of mechanisms, meets this principle. Traditional objects are useful for purpose of geological mapping mainly but not for study of its mechanisms formation. 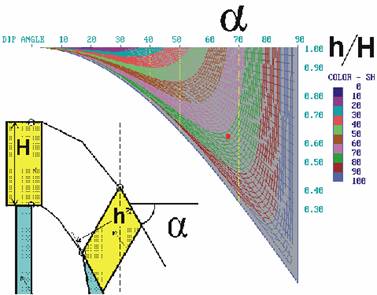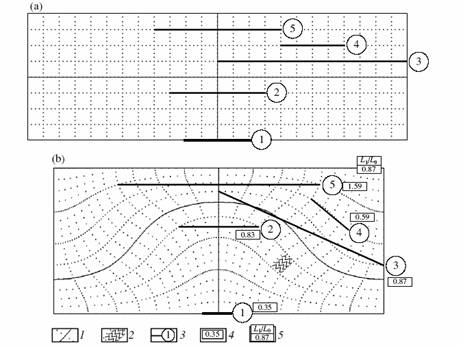The path of investigation includes study small objects at first and the using these data in study of larger objects (for instance, shortening value of folds uses in study of folded domains, Fig. 4). 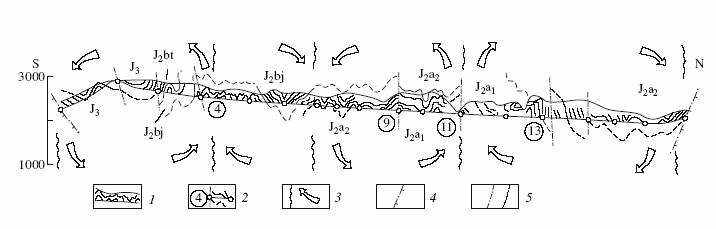Thus folded domains, structural cells and tectonic zones are investigating in series (Fig. 5, 6). The proposed method makes it possible to obtain reliable new data on the linear folding and their formation mechanisms. The method also allows us to determined reliably shortening values for these structures.

Publications. Yakovlev F. L. Multirank Strain Analysis of Linear Folded Structures // Doklady Earth Sciences, 2008a, Vol. 422, No. 7, pp. 1056–1061. PDF, (N 28 in En-List). Full information is in paper (Yakovlev F.L. Quantitative methods of analysis of natural formations mechanisms for folds and for systems of linear folding // Problems of tectonophysics. To fortieth anniversary of foundation by M.Gzovsky the Tectonophysics Laboratory in the Institute of physics of the Earth RAS. / Moscow. Publishing of IPE RAS. 2008b. pp. 149 – 188. [in Russian] PDF-R; N 35 in En-List)


Fig. 1. Usual separate fold – single viscous layer folds. This kind of structure has correct mechanical model of formation. The shape of folds is using for reverse problem solution – for the finding out the shortening value and viscosity contrast.	Fig. 2. The separate fold – multilayer folds as combination of competent and incompetent layers. Set of cinematic mechanisms was used for creation of cinematic model of its forming.	Fig. 3. The monogram for finding out of shortening value (SH or ε3 for domain) of multilayer folds, based on cinematic model of its forming. Simple parameters of fold shape is using: dip of bed on the flank, thicknesses of layer on flank and on hinge. Position of point on isolines show the SH regarding the perpendicular to axial plain.	Fig. 4. Folded domain (new object) consists of numerous folds. It is main object for the folding analysis. There is ellipsoid of strain for folded domain (Ax – axial surface dip(3), En –envelope surface dip(2), Sh – shortening value (4, ε3). 1 - horizontal plain

Fig. 6. Relations between different-rank structures exemplified by the section across the Tfan tectonic zone of the southeastern Caucasus ([Yakovlev, 2008a]). The section comprises 17 domains and 4 structural cells. ( 1 ) Individual folds; ( 2 ) boundaries and number of the domain;
( 3 ) boundaries of structural cells and general direction of matter movement in them; ( 4 ) boundaries of the tectonic zone; ( 5 ) large and minor faults.

Fig. 4. The structural cell as a minimal structure, shortening of which corresponds to the tectonically determined horizontal shortening of the sedimentary cover Caucasus ([Yakovlev, 2008a]). (a) Two neighboring cells in the initial state; (b) the same cells after the action of quasi-buckling (combination of advection and flattening). ( 1 ) Initial grid and its distortion (the solid line retains its length); ( 2 ) symbolic image of folds within a conventional folded domain; ( 3 ) segment and its number; ( 4 ) horizontal Sh value for the segment; ( 5 ) value of integral shortening for cells. The model shows strain heterogeneity in horizontal shortening for different structures within cells. Contraction coincides with integral shortening only for segment 3.